Giá trị trung bình của dòng điện xoay chiều AC
Giá trị trung bình của dạng sóng xoay chiều như sóng hình sin, khi lấy trong một chu kỳ đầy đủ, bằng 0. Điều này là do, dạng sóng hình sin, là sóng xoay chiều tức là nó đối xứng qua trục X và các giá trị ở nửa dương. hủy các giá trị ở nửa âm khi lấy giá trị trung bình
Giá trị trung bình của các giá trị tức thời của dạng sóng AC được tính trong nửa chu kỳ. Thiết bị đo thông thường phản hồi với giá trị trung bình.
Đối với sóng hình sin:
Giá trị trung bình = Giá trị lớn nhất × 2 / π = Giá trị lớn nhất × 0,637
Khi giá trị True RMS là 100V;
Giá trị trung bình = Giá trị lớn nhất × 2 / π = 141 × 0,637 = 90 (V)
Số đọc của thiết bị đo thông thường được hiệu chỉnh theo giá trị hiệu dụng của sóng hình sin mặc dù họ đang đáp ứng với giá trị trung bình. Chúng được gọi là loại máy thử nghiệm được hiệu chuẩn theo RMS phản hồi trung bình. Trái ngược với những điều này, người kiểm tra loại true RMS phản hồi và hiển thị giá trị True RMS.
Tính toán độ lớn của các đại lượng xoay chiều như dòng điện hoặc điện áp trong xoay chiều không phải là một công việc thẳng như trong điện một chiều, nơi các giá trị không đổi theo thời gian. Có một số phương pháp để biểu diễn độ lớn của dạng sóng xoay chiều. Trong trường hợp dạng sóng xoay chiều hình sin, cường độ của điện áp và dòng điện có thể được biểu diễn bằng
Giá trị cao
Giá trị đỉnh – đến – đỉnh
Giá trị RMS
Giá trị tức thời
(Các giá trị này có thể được sử dụng để biểu thị độ lớn của thậm chí bất kỳ dạng sóng tuần hoàn nào khác)
Có một cách khác để biểu diễn độ lớn của dạng sóng AC. Nó được gọi là Giá trị trung bình.
Các giá trị của điện áp trung bình và dòng điện trung bình của sóng hình sin xoay chiều có thể hữu ích trong nhiều hoạt động phân tích mạch. Trên thực tế, loại chỉnh lưu nhiều đồng hồ đo điện áp trung bình của AC và sau đó thực hiện một số tính toán trên đó và hiển thị đầu ra dưới dạng giá trị RMS.
Điện áp trung bình
Điện áp trung bình, như tên chỉ ra, là giá trị trung bình của điện áp tức thời được chọn ở những khoảng thời gian thích hợp trong nửa chu kỳ của dạng sóng xoay chiều hình sin (hoặc bất kỳ tuần hoàn nào khác). Giá trị trung bình đại diện cho thương số của diện tích dưới dạng sóng AC theo thời gian.
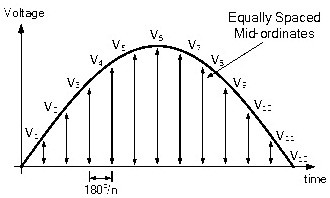
Để tìm hiệu điện thế trung bình của một dạng sóng xoay chiều, người ta chia nửa chu kỳ thành các hoành độ cách đều nhau. Điện áp tức thời tại các điểm giữa này được tính. Bằng cách tính giá trị trung bình của các giá trị điện áp tức thời này, chúng ta nhận được giá trị trung bình của dạng sóng AC (cho dù là điện áp hay dòng điện).
Việc xác định giá trị điện áp trung bình của dạng sóng xoay chiều tương tự như việc tìm điện áp RMS của dạng sóng xoay chiều. Nhưng trong quá trình tìm hiệu điện thế trung bình, không cần tìm bình phương của các điện áp tức thời. Chúng ta có thể tìm thấy giá trị điện áp trung bình của bất kỳ hình dạng sóng nào.
Giá trị điện áp trung bình có thể được nói là “Thương số của diện tích dưới đường cong (sóng sin hoặc sóng vuông hoặc bất kỳ sóng tuần hoàn nào khác) tại bất kỳ thời điểm nào” hoặc chúng ta cũng có thể nói “Trung bình của tất cả các giá trị điện áp tức thời là được gọi là Điện áp trung bình ”.
Mọi dạng sóng tuần hoàn đều có hình dạng đối xứng tức là sẽ có nửa chu kỳ dương và nửa chu kỳ âm. Diện tích của nửa chu kỳ dương luôn bằng và ngược dấu với diện tích của nửa chu kỳ âm.
Tổng các vùng trong cả hai nửa chu kỳ được trả về Zero, vì các vùng âm và dương hủy bỏ từng vùng. Do đó, giá trị trung bình được tính bằng cách chỉ xem xét một nửa chu kỳ.
Giá trị điện áp trung bình chỉ được đo trong một nửa chu kỳ của dạng sóng tuần hoàn hoàn chỉnh. Điện áp trung bình còn được gọi là “Điện áp trung bình của dạng sóng”.
Giá trị trung bình có thể được tìm thấy cho cả phân tích và tính toán mạch AC và DC. Giá trị trung bình được biểu thị bằng VAVG cho điện áp trung bình và IAVG cho dòng điện trung bình.
Khái niệm về giá trị tức thời
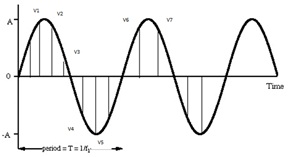
Giá trị tức thời (điện áp hoặc dòng điện) của dạng sóng xoay chiều là giá trị tại bất kỳ thời điểm cụ thể nào. Điện áp của một dạng sóng tại một thời điểm nhất định được gọi là “Điện áp tức thời”.
Trong sơ đồ trên, V1, V2, V3, V4… là điện áp tức thời của sóng sin. Để tìm giá trị điện áp tức thời của sóng hình sin, ta phụ thuộc vào điện áp cực đại của sóng hình sin.
Điện áp tức thời = Điện áp cực đại x sin θ
V INST = V MAX x sin θ
Ở đây, θ là góc mà tại đó các điểm giữa được tạo thành. Ví dụ, trong trường hợp sóng hình sin xoay chiều, góc lớn nhất là 1800 đối với nửa chu kỳ dương. Nếu chúng ta chia nửa chu kỳ thành 10 trung điểm, thì θ sẽ là bội số của 1800/10 = 180 tức là θ lấy 180, 360, 540… .lên 1800.
Điện áp trung bình của dạng sóng trong phương pháp đồ thị
Giá trị trung bình của dạng sóng xoay chiều như sóng hình sin, khi lấy trong một chu kỳ đầy đủ, bằng 0. Điều này là do, dạng sóng hình sin, là sóng xoay chiều tức là nó đối xứng qua trục X và các giá trị ở nửa dương. hủy các giá trị ở nửa âm khi lấy giá trị trung bình.
Nhưng giá trị trung bình của điện áp và dòng điện hình sin không thể bằng 0 trong thời gian thực. Do đó, giá trị trung bình của một giá trị xoay chiều có thể được tính bằng cách lấy giá trị trung bình của các giá trị tức thời cách đều nhau của nửa chu kỳ của dạng sóng xoay chiều.
Quá trình này tương tự như quá trình tìm điện áp RMS. Nửa chu kỳ dương được chia đều thành n phần với khoảng cách giữa chúng bằng nhau. Các phần được chia đều được gọi là “Giá trị giữa” và giá trị thương số này của mỗi phần được gọi là “Giá trị tức thời”.
Mỗi giá trị thứ tự giữa của một dạng sóng xen kẽ được thêm vào giá trị của thứ tự tiếp theo của nó và tổng số cộng thêm được chia cho tổng số thứ tự giữa. Đây là giá trị của điện áp trung bình. Điện áp trung bình được cho bởi công thức dưới đây.
Ví dụ, nếu chúng ta đã chia nửa chu kỳ thành 10 bậc bằng nhau, thì điện áp trung bình có thể được tính là
Nếu chúng ta coi một sóng xoay chiều biểu diễn một điện áp xoay chiều có hiệu điện thế cực đại là 340v, thì hiệu điện thế trung bình có thể được tính như sau.
Chia đường cong thành 10 điểm giữa và tính điện áp tức thời tại các điểm đó.
Sử dụng công thức trên, điện áp trung bình có thể được tính như
Vavg = 2146/10 = 214,6 vôn
Do đó, giá trị điện áp trung bình là 214,6 vôn.
Điện áp trung bình của dạng sóng trong phương pháp phân tích
Như chúng ta đã biết, mọi dạng sóng tuần hoàn đều có giá trị trung bình của nó là tổng bằng 0 vì nó có các phần bằng nhau của nửa chu kỳ dương và âm. Giá trị trung bình có thể được tính bằng cách xem xét giá trị tức thời chỉ của một nửa chu kỳ thay vì tất cả các giá trị tức thời.
Điều này chỉ áp dụng cho các dạng sóng đối xứng như sóng hình sin. Trong điện áp không đối xứng, chúng ta nên tính giá trị trung bình của các điện áp tức thời cho chu kỳ hoàn chỉnh của dạng sóng tuần hoàn, để tìm ra giá trị chính xác.
Khoảng cách của khu vực
Để tìm giá trị trung bình, chúng ta cần tính diện tích gần đúng của dạng sóng hoặc đường cong tại một số khoảng thời gian. Để tìm diện tích của đường cong, người ta chia nó thành nhiều hình chữ nhật hoặc hình tam giác nhỏ. Bằng cách tính gần đúng diện tích của các hình chữ nhật riêng lẻ này và cộng tất cả các diện tích này, giá trị trung bình có thể được tính toán.
Độ chính xác của giá trị trung bình có thể được tăng lên bằng cách xem xét một số lượng hình chữ nhật nhỏ vô hạn (rất lớn). Biểu đồ sau đây biểu diễn mức trung bình của diện tích được bao phủ dưới đường cong với các hình chữ nhật nhỏ ở các khoảng thời gian bằng nhau của dạng sóng.
Bằng cách tính giá trị trung bình của diện tích dưới đường cong, chúng ta có thể tìm được giá trị chính xác của giá trị điện áp trung bình. Giá trị chính xác nhất sẽ xuất hiện khi giá trị này tiếp cận 2Π.
Có nhiều phương pháp để tính gần đúng giá trị của diện tích dưới đường cong. Đó là quy tắc hình thang, quy tắc trung gian, quy tắc Simpson, vv Nếu chúng ta coi một sóng sin điện áp xoay chiều, nó được biểu diễn dưới dạng V (t) = Vp.cos (ωt). Diện tích dưới đường cong ở mọi trường hợp được toán học đưa ra là
Diện tích = V p Sin (wt) dt
Ở đây, T là khoảng thời gian của dạng sóng tuần hoàn và các giới hạn của tích phân là 0 và Π vì chúng ta chỉ xem xét nửa chu kỳ.
Sử dụng công thức trên, chúng ta có thể tính diện tích dưới dạng sóng và chúng ta nhận được rằng
Diện tích = 2V P .
Bây giờ, chúng ta biết diện tích dưới nửa chu kỳ dương (hoặc nửa chu kỳ âm), chúng ta có thể dễ dàng tính giá trị trung bình (điện áp hoặc dòng điện) của sóng hình sin xoay chiều tuần hoàn bằng cách tích phân đại lượng sin theo chu kỳ dương (hoặc âm) và chia nó với khoảng thời gian.
Ví dụ, nếu chúng ta có điện áp tức thời của sóng xoay chiều là V = Vp.sinθ với khoảng thời gian 2Π thì điện áp trung bình của dạng sóng xoay chiều là
V AV = 1 / Π V p Sin (Φ) dΦ
V AV = V p / Π -cos (Φ)
= 2V p / Π = 0,673V p
Phương trình điện áp trung bình
Giá trị điện áp trung bình của dạng sóng xoay chiều được cho bởi
V AV = 2V p / Π = 0,673V p
Vậy giá trị trung bình của sóng hình sin xoay chiều bằng phép nhân giá trị điện áp đỉnh với 0,637.
Như ví dụ đã thảo luận ở trên, nếu chúng ta có một sóng hình sin với điện áp cực đại (đỉnh) là 340 Volts, thì giá trị điện áp trung bình có thể được tìm thấy trong phương pháp phân tích được đưa ra dưới đây.
V AV = V PEAK x 0,637 = 340 x 0,637 = 216,5 V.
Giá trị của điện áp RMS tính theo điện áp đỉnh là V RMS = 0,707 x V PEAK . So sánh điện áp trung bình và RMS được hiển thị bên dưới.
LƯU Ý: Nhân giá trị đỉnh với 0,637 chỉ áp dụng cho sóng hình sin, không áp dụng cho các dạng sóng khác như sóng răng cưa và sóng tam giác.
Tầm quan trọng của giá trị trung bình trong phép đo dạng sóng hình sin AC
Bộ chỉnh lưu đa đồng hồ chỉ ra các giá trị RMS (điện áp hoặc dòng điện) chỉ cho sóng hình sin. Giá trị RMS được tính trước tiên bằng cách tính Giá trị trung bình và sau đó nhân với 1,11. Nếu chúng ta sử dụng đồng hồ đa năng này để đo giá trị RMS của bất kỳ dạng sóng Xen kẽ nào khác, kết quả sẽ là giá trị RMS sai.
Tóm lược
Dạng sóng thay đổi hướng theo chu kỳ được gọi là “Dạng sóng xoay chiều” hoặc “Dạng sóng AC”.
Các thủ tục tìm giá trị RMS và giá trị trung bình của dạng sóng xoay chiều là tương tự.
Chúng tôi tính giá trị trung bình bằng cách chỉ xem xét nửa chu kỳ của dạng sóng xoay chiều.
Có hai phương pháp để tính giá trị trung bình của dạng sóng AC hoặc dạng sóng xoay chiều. họ đang
1. Phương pháp phân tích
2. Phương pháp đồ thị
Đối với phương pháp đồ thị, công thức để tìm hiệu điện thế trung bình là
Đối với phương pháp phân tích, công thức cho giá trị điện áp trung bình là
Mối quan hệ giữa điện áp trung bình và giá trị điện áp lớn nhất hoặc giá trị điện áp đỉnh được cho là “Điện áp trung bình bằng 0,637 lần điện áp đỉnh”.
V AVG = V PEAK x 0,637